Article

Computer Modelling for Better Diagnosis and Therapy of Patients by Cardiac Resynchronisation Therapy

Register or Login to View PDF Permissions
Permissions× For commercial reprint enquiries please contact Springer Healthcare: ReprintsWarehouse@springernature.com.

For permissions and non-commercial reprint enquiries, please visit Copyright.com to start a request.

For author reprints, please email rob.barclay@radcliffe-group.com.
Information image

  • Views: 25

  • Likes: 0

  • Read time: 15m
Average (ratings)
No ratings
Your rating

Abstract

Mathematical or computer models have become increasingly popular in biomedical science. Although they are a simplification of reality, computer models are able to link a multitude of processes to each other. In the fields of cardiac physiology and cardiology, models can be used to describe the combined activity of all ion channels (electrical models) or contraction-related processes (mechanical models) in potentially millions of cardiac cells. Electromechanical models go one step further by coupling electrical and mechanical processes and incorporating mechano-electrical feedback. The field of cardiac computer modelling is making rapid progress due to advances in research and the ever-increasing calculation power of computers. Computer models have helped to provide better understanding of disease mechanisms and treatment. The ultimate goal will be to create patient-specific models using diagnostic measurements from the individual patient. This paper gives a brief overview of computer models in the field of cardiology and mentions some scientific achievements and clinical applications, especially in relation to cardiac resynchronisation therapy (CRT).

Keywords

Computer model, bidomain model, monodomain model, finite element model, cardiac resynchronisation therapy, heart failure,

Disclosure:Marieke Pluijmert, Mark Potse and Tammo Delhaas have no conflicts of interest to declare. Angelo Auricchio is a consultant to Biosense Webster, Biologics Delivery Systems Group, Bristol-Myers Squibb, DC Devices, EBR Systems, Infobionics, Leadexx, Medtronic, Resmed and Sorin Group. He has received speaker fees from Biotronik GmBH, Medtronic, Resmed and Sorin Group. Joost Lumens received a grant within the framework of the Dr E Dekker programme of the Dutch Heart Foundation (NHS-2012T010). Frits W Prinzen has received research grants from Boston Scientific, Biologics Delivery Systems Group, Cordis Corporation, EBR Systems, Medtronic, MSD, Proteus Biomedical and St Jude Medical.

Received:

Accepted:

Correspondence Details:Frits W Prinzen, Professor of Physiology, Maastricht University, P.O. Box 616, 6200 MD, Maastricht, The Netherlands. E: frits.prinzen@maastrichtuniversity.nl

Open Access:

This work is open access under the CC-BY-NC 4.0 License which allows users to copy, redistribute and make derivative works for non-commercial purposes, provided the original work is cited correctly.

The number of cardiac devices being implanted, especially cardiac resynchronisation therapy (CRT) pacemakers and implantable cardioverter defibrillators (ICDs), continues to rise. Important determinants of the clinical benefit of CRT are the electrical and structural substrate and the site of implantation. While clinical studies and experimental work have provided a large amount of evidence for certain approaches, evidence is lacking in some areas, particularly regarding mechanisms of disease. Large inter-patient variability exists and so there is a quest to tailor therapy to the individual patient. It is here that computer models may assist in the diagnosis and the design of the therapy.

By definition, models are simplified representations of reality. Such simplification can help to identify important features of a (patho-)physiological process, although the same simplification may also lead to erroneous interpretation of observations when boundaries of validity, determined by fundamental model assumptions, are ignored. The value of a model can be illustrated by the example of Einthoven’s triangle for interpretation of the electrocardiogram (ECG), proposed by this Dutch investigator more then a century ago (see Figure 1).1 It assumes the human body to be an equilateral triangle, with uniform electrical conduction and the heart in the middle. All three assumptions are clearly wrong, but this model is still used in everyday practice, because many aspects of the ECG and its frontal leads can be well understood through its use. However, the Einthoven triangle model is not accurate enough to predict highly localised electrical abnormalities. To paraphrase Einstein: ‘a model has to be as simple as possible, but not simpler’.

Figure 1: Einthoven’s Triangle as an Example of a Simple Model

Article image
Download

It is crucial to be aware of the assumptions made in the creation of simple models, while recognising that fair predictions may often be made by such models. Mathematical models have become more complex due to increasing computing power and greater quantities of experimental data. This development carries the risk that models become so complicated that the investigator may not know exactly what is going on. At this point the model may become a black box, which is not so different from an in vivo experiment. Therefore, it seems justified to state that ‘a model has to be as complicated as necessary, but not more complicated’. In other words, it seems wise to choose a model that best suits the research question.

Electrophysiological Models

The entire process of electromechanical activation starts with the action potential. It is now more than 50 years since Hodgkin and Huxley developed their model of the action potential of the squid giant axon,2 which is the basis for current mathematical models of cardiac electrophysiology.

Nowadays a series of electrophysiological models for cardiac muscle cells are available, with key differences from one another.3 These single cell models can be coupled using simulated gap junctions to predict interactions between cells, such as propagation of the action potential and repolarisation.

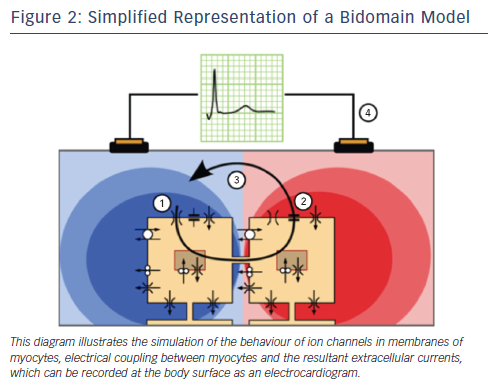
In whole heart models, electrophysiological properties are most accurately described when a distinction is made between the intracellular and interstitial domains. In the so-called bidomain equations conductive properties of cardiac tissue are modelled as a combination of these two domains (see Figure 2). Bidomain models can simulate the effects of external stimuli and defibrillation currents,4,5 as well as predict the smaller and prolonged calcium transients and action potential duration (APD) observed in myocytes from failing hearts.6

Figure 2: Simplified Representation of a Bidomain Model

Article image
Download

Electrical models need high temporal and spatial resolution, due to the steepness of the membrane potential upstroke and the resulting steep spatial potential gradients. Consequently, published models of the human heart have 10–100 million elements.7,8 These models can calculate all the electrical processes, ranging from ion currents at the cellular level to body surface ECGs, in which the heart is simulated to be within a chest model.

If impulse propagation alone is to be computed, the eikonal diffusion equation can be used. This equation is derived from the bidomain model and solves only for activation times. This approach is computationally less demanding and has been successfully applied in finite-element models of the heart that focus on mechanics.9

Some Achievements of Electrical Models

In bidomain models, a larger heart size decreases global electrotonic effects and unmasks intrinsic APD differences between cell types, thus increasing APD dispersion.10 Similarly, a high-resolution magnetic resonance imaging (MRI)-based rabbit heart model was able to mechanistically demonstrate the role of blood vessels and endocardial trabeculations in ventricular impulse propagation.11 These results underscore the regional differences in activation attributable to shortcut pathways and indicate the important role that microstructure of the heart may play in impulse propagation. A host of literature now describes computer-modelling studies in cardiac arrhythmias and their resolution by defibrillation, which has been reviewed recently.4

Potse et al. used a reaction diffusion model that enabled investigation of the entire chain, from cellular cardiac electrophysiology to body-surface ECG signals and endocardially derived electrograms.5,12 This model has been used for questions relating to Brugada syndrome13 and ST-segment analysis in infarcted hearts.14,15 More recently, the model was used to better understand the effect of decreased tissue conductivity on ventricular activation pattern and QRS morphology. Conductivity reduction in the left ventricular (LV) wall, as in the case of pressure overload hypertrophy,16 resulted in a significant left axis deviation in the frontal plane of the ECG and a moderate increase in QRS duration. The simulated ECG had a morphology similar to left bundle branch block (LBBB) but with a much lower amplitude.8 Combination of LBBB and low conductivity resulted in an unchanged (LBBB-specific) conduction pattern in combination with prolonged but smaller QRS complexes.8 Small QRS amplitudes may thus indicate ‘low quality’ myocardium and may indicate increased risk of arrhythmias,17 an important indicator for ICD need in a CRT candidate. This model observation may be used to improve interpretation of the ECG. Particularly in the case of serial ECG measurements, detailed information about electrical and structural remodelling may be deciphered by analysing QRS duration, morphology and amplitude.

In order to create patient-specific models, the patients’ anatomy is reconstructed using MRI or computed tomography (CT) scans. While fibre and sheet orientation are important for impulse propagation, these data are usually not available for individual patients, and so the fibre orientations in the models are commonly rule-11 or atlas-based.18 Subsequently, parameters describing impulse conduction are adjusted until the predicted activation sequence mimics that measured using endocardial mapping. Niederer et al. have described this process for a single patient.19

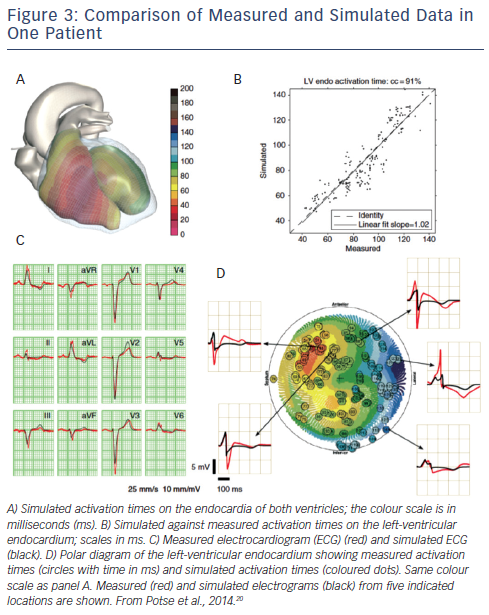
Electrophysiological verification can be performed using both surface ECG and cardiac electrograms.20 Parameters of the bidomain model were adjusted to match activation times measured at the LV endocardium and the morphology of the body surface ECG. Important steps were removal of the Purkinje system in the LV and the choice of location of earliest activation in the right ventricular (RV) wall, as well as adjustment of myocardial conductivity. While these steps resulted in close approximation to the measured activation sequence and QRS complex, repolarisation parameters were adjusted to match the T wave (see Figure 3). Heterogeneity in the maximum conductivity of the slow delayed rectifier current (IKs) was introduced using an inverse linear relation with the depolarisation time, mimicking a ‘ventricular gradient’. The slope of this relationship was used to tune the T-wave amplitude. The maximum conductivity of the inward rectifier current (IK1) was reduced to blunt the peaks of the T waves. Model-fitting in patients with dyssynchronous heart failure suggests that in these hearts there is no retrograde conduction of the electrical impulse from the working myocardium into the Purkinje system, that myocardial conductivity is considerably lower than in normal myocardium and that a ventricular gradient is at least partially preserved.20

Figure 3: Comparison of Measured and Simulated Data in One Patient

Article image
Download

Mechanical Models

The deformation of the heart during the cardiac cycle is determined by the mechanical equilibrium between forces developed by active contraction of the myofibres, passive stretch of the connective tissue matrix, pressure in the cardiac cavities and pressure exerted by the pericardium. Mathematical models of cardiac mechanics help to improve understanding of these complex interactions under (ab)normal conditions. Early model studies indicated that myofibre orientation is an important determinant of local myocardial tissue stress and strain.21–23

It was demonstrated that fibre stress and strain during systole are likely to be distributed homogeneously across the wall. Based on this assumption of homogeneity, the ‘one-fibre model’ was developed that relates local myofibre mechanics, in terms of fibre stress and strain, to global cardiac pump mechanics, in terms of cavity pressure and volume.24 This relatively simple but well-designed model is the basis of the CircAdapt model.25 More recent versions use a biventricular model of the heart that provides important and reliable information about the mechanical interaction between the two ventricles.26–28

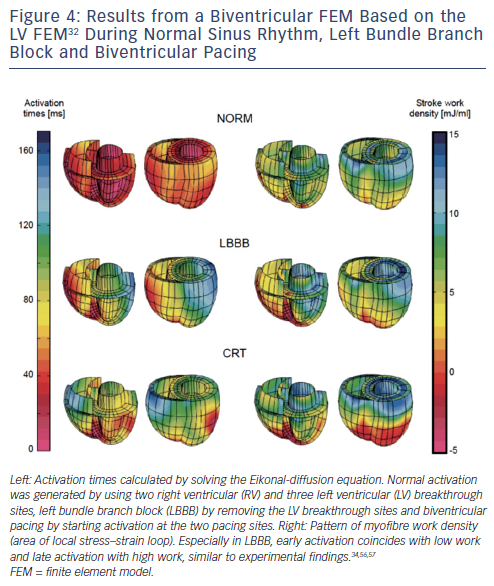
For a more detailed analysis of deformations in 3D, finite element models (FEM) have been developed.29,30 FEMs account for the spatial variation in myofibre and sheet orientation across the walls.31 Most studies have implemented a rule-based variation in fibre orientation. Alternatively, the myofibre orientation can be allowed to change locally in response to local fibre cross-fibre shear until they achieve a preferred mechanical loading state.32 This adaptation in fibre orientation leads to a more homogeneous strain distribution and improved pump function. Figure 4 shows preliminary results of activation times and distribution of mechanical work in a normal heart and hearts with LBBB and with CRT.

Figure 4: Results from a Biventricular FEM Based on the LV FEM32 During Normal Sinus Rhythm, Left Bundle Branch Block and Biventricular Pacing

Article image
Download

Some Achievements of Mechanical Models

When applied to the case of asynchronous activation, models of cardiac mechanics were able to simulate the characteristic relationship between activation and mechanics that has been observed in experiments33,34 and patients.35,36 In early-activated regions, a rapid early systolic fibre shortening was found, followed by strongly reduced late systolic shortening. Later-activated regions were characterised by early systolic lengthening followed by pronounced systolic shortening.37,38

These models proved helpful for understanding the observed deformation patterns. Using a FEM, Kerckhoffs et al.39 simulated various combinations of dilatation, systolic and diastolic heart failure and dyssynchrony in order to evaluate the performance of various indices of mechanical dyssynchrony (circumferential uniformity ratio estimate [CURE],40 internal stretch fraction [ISF]41 and time delay in peak shortening between opposing walls [the most frequently used measure]). CURE and ISF, metrics of distribution of strain magnitudes, were sensitive to the combination of activation sequence and dilatation, whereas time to peak shortening was not.42

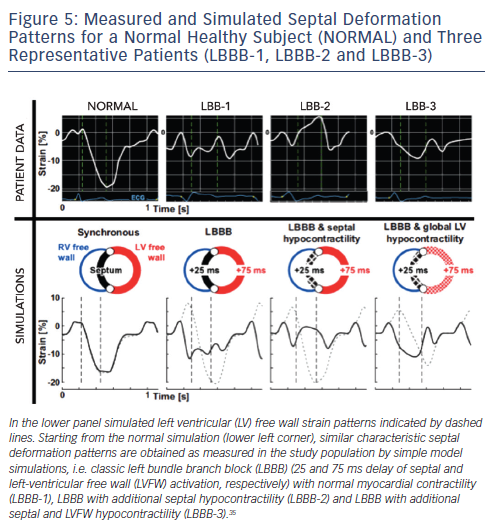
Leenders et al. studied the mechanism of the septal strain patterns in LBBB patients. Using the CircAdapt model containing wall segments representing the RV free wall, septum and LV free wall, they were able to demonstrate how double-, early- and late-peak septal strain patterns could originate from different combinations of a true electrical substrate of mechanical dyssynchrony whether or not in combination with regional differences in myocardial contractility (see Figure 5).35 A recent clinical study supported these findings and showed that double-and early-peak septal strain patterns are highly predictive for CRT response.43

Figure 5: Measured and Simulated Septal Deformation Patterns for a Normal Healthy Subject (NORMAL) and Three Representative Patients (LBBB-1, LBBB-2 and LBBB-3)

Article image
Download

In another CircAdapt study, during gradual pre-excitation of the septum compared with the LV free wall, the time to peak shortening in the septum shortened in two major steps, providing a poor quantitative reflection of true dyssynchrony.36 Together with the data published by Kerckhoffs et al.42 these observations plead for the use of parameters of dyssynchrony that describe the shortening/deformation pattern rather than the time to peak shortening.

A recent study with the CircAdapt model compared the haemodynamic effects of LV and biventricular pacing, supported by measurements in patients and in the canine model of dyssynchronous heart failure. LV pacing consistently provided similar haemodynamic benefit to biventricular pacing, despite the larger dyssynchrony (though opposite to that during LBBB). The model was able to provide an explanation for this paradoxical finding: LV pacing results in pre-stretching of the RV free wall, which subsequently increases its workload, thereby supporting the LV in its pump function through mechanical ventricular interaction.28

Electromechanical Models

Various electromechanical models of the ventricles have been reviewed extensively elsewhere.44 Historically, large-scale models were aimed at either electrophysiology or mechanics. As a consequence, most combined models are weakly coupled, i.e. electrophysiology (in particular activation sequence) is computed separately from mechanical behaviour. In its ultimate form, models of cardiac electromechanics properly describe the physical and physiological processes linking cardiac electrophysiology and mechanics, i.e. calcium handling and cross-bridge formation. Here, models describing the calcium-force relation come into play, such as those developed by Rice45 and Niederer.46

 

Models that implement the effect of mechano-electrical feedback in the generation of arrhythmias47 are a further step in the complete integration of electromechanics. A similarly integrated approach is required in studies on local mechanical load as a determinant of local APD and contractility.48,49

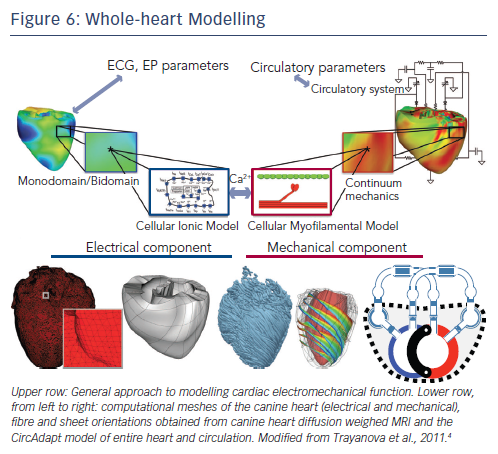
Medically relevant models for device therapy, especially CRT, are required to cover many aspects. Abnormal electrical impulse conduction (requiring electrophysiological models) gives rise to abnormal contraction (to be captured by mechanical models), which leads to worsening pump function (calculated by haemodynamic models, preferably of the entire circulation). Moreover, heart failure may lead to complicated molecular and cellular remodelling, which require models linking these subcellular processes with properties at the tissue and organ level. Figure 6 shows many of the processes that may need to be measured and modelled when studying dyssynchronous heart failure and application of CRT. Clearly, implementing this all in a model is a huge undertaking.

Figure 6: Whole-heart Modelling

Article image
Download

Some Results from Electromechanical Models

Early electromechanical measurements indicated that the time interval between depolarisation and the onset of muscle shortening (electromechanical delay [EMD]) was longer in late- than in early-activated regions of paced ventricles.50 Later measurements51 indicated that EMD is larger in the subepicardium than in the subendocardium. Computer models indicated that the more pronounced a region was prestretched, the longer was its EMD.7,37 The most detailed study on this topic used a combination of measurements in animals in situ, isolated trabeculae, patients and a computer model. These studies provided evidence that it is not prestretch itself but the rate of rise of LV pressure (LV dP/dtmax) at the time of depolarisation that is the direct determinant of the length of EMD.52 This group also showed that the use of a measure of ‘true active force development’ rather than onset of shortening, provides a delay between electrical and mechanical activation that is independent of timing of activation or ischaemia.53

As a large portion of CRT non-responders are heart failure patients with chronic myocardial infarction, it is important to understand the impact of the infarct on cardiac dyssynchrony and resynchronisation. Kerckhoffs et al. demonstrated that increased infarct scar size diminishes the improvement of ventricular function following biventricular CRT in the LBBB failing heart.54 In these simulations, however, impulse conduction was not influenced by the scar tissue.

Niederer employed bidomain modelling to investigate a combination of two effects: scar and multisite pacing. Postero-lateral scar was simulated in two severities, creating a 50 % and 90 % reduction in conductivity, thus implementing the slower conduction in the scar. This study indicated that, in the presence of postero-lateral scar, multisite pacing offers a better haemodynamic response than conventional CRT. This effect was associated with a larger LV activation wave, as induced by multisite pacing.55

Future Perspectives

As discussed above, studies using computer models have primarily contributed to better understanding mechanistic aspects of cardiac electromechanics. The ultimate goal of the modelling work is, however, to serve as a system that supports clinical decision-making and thereby to improve diagnosis and therapy planning. Nowadays, patients with heart disease undergo a large number of diagnostic measurements, such as ECG, echocardiography, CT and/or cardiac MRI. Each of these modalities provides some information about the heart and circulation, but in order to achieve the complete picture of the disease, data of different modalities need to be combined. Computer models are able to handle this complex dataset quite well, thereby improving diagnosis and healthcare, for example in the better selection of CRT patients and improved therapy planning.

Reality forces us to acknowledge that there is still a long way to go. Patient-specific models that fully and reliably replicate an individual patient’s characteristics and affect the clinicians’ diagnostic and therapeutic work-up are still under development. Part of the problem is that the data used for the mathematical description of these physiological principles have been derived from animal myocardium models (from species ranging from mouse to dog), often from isolated cells and membrane patches kept in specific solutions and sometimes at temperatures different from body temperatures. As a consequence, the values obtained in isolated set-ups may not be those prevalent in real life. It is the experience of many builders of computer models that, even after years of work meticulously connecting many molecular properties, the calculated final physiological signal, such as action potential or LV pressure curve, deviates from measured ones. Frequently, therefore, gaps are filled by new model parameters, allowing to adjust (or tweak) the model predictions to the real measurements. While this may appear disappointing, the true scientific merit of this is that computer models help us to ‘know what we do not know’. And for a complicated chain of processes, from ion channels contributing to membrane potential through calcium and contraction to total cardiac pump function, we have to acknowledge that there are many uncertainties to solve. Nevertheless, as mentioned in the introduction, relatively simple problems may already be solved with relatively simple models.

References

  1. Einthoven W, Fahr G, de Waart A. Über die Richtung und die manifeste Grösse der Potentialschwankungen im menschlichen Herzen und Über den Einfluss der Herzlage auf die Form des Elektrokardiogramms. Pflüger Arch ges Physiol 1913;150:275–315.
  2. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 1952;117:500–44.
  3. Niederer SA, Fink M, Noble D, Smith NP. A meta-analysis of cardiac electrophysiology computational models. Exp Physiol 2009;94.5:486–95.
  4. Trayanova NA. Whole-heart modeling: applications to cardiac electrophysiology and electromechanics. Circ Res 2011;108:113–28.
  5. Potse M, Dube B, Richer J, et al. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans Biomed Eng 2006;53:2425–35.
  6. Priebe L, Beuckelmann DJ. Simulation study of cellular electric properties in heart failure. Circ Res 1998;82:1206–23.
  7. Gurev V, Constantino J, Rice JJ, Trayanova NA. Distribution of electromechanical delay in the heart: insights from a three-dimensional electromechanical model. Biophys J 2010;99:745–4.
  8. Potse M, Krause D, Bacharova L, et al. Similarities and differences between electrocardiogram signs of left bundlebranch block and left-ventricular uncoupling. Europace 2012;Suppl 5:v33–9.
  9. Colli-Franzone P, Guerri L,Tentoni S. Mathematical modeling of the excitation process in myocardial tissue: influence of fiber rotation on wavefront propagation and potential field. Math Biosci 1990;101:155–235.
  10. Sampson KJ, Henriquez CS. Electrotonic influences on action potential duration dispersion in small hearts: a simulation study. Am J Physiol Heart Circ Physiol 2005;289:H350–60.
  11. Bishop MJ, Plank G, Burton RA, et al. Development of an anatomically detailed MRI-derived rabbit ventricular model and assessment of its impact on simulations of electrophysiological function. Am J Physiol Heart Circ Physiol 2010;298:H699–718.
  12. Potse M, Vinet A, Opthof T, Coronel R. Validation of a simple model for the morphology of the T wave in unipolar electrograms. Am J Physiol Heart Circ Physiol 2009;297:H792–801.
  13. Hoogendijk MG, Potse M, Vinet A, et al. ST segment elevation by current-to-load mismatch: an experimental and computational study. Heart Rhythm 2011;8:111–8.
  14. Hoogendijk MG, Potse M, Linnenbank AC, et al. Mechanism of right precordial ST-segment elevation in structural heart disease: Excitation failure by current-to-load mismatch. Heart Rhythm 2010;7:238–48.
  15. Potse M, Coronel R, Falcao S, et al. The effect of lesion size and tissue remodeling on ST deviation in partial-thickness ischemia. Heart Rhythm 2007;4:200–6.
  16. Severs NJ, Bruce AF, Dupont E, Rothery S. Remodelling of gap junctions and connexin expression in diseased myocardium. Cardiovasc Res 2008;80:9–19.
  17. Danik SB, Liu F, Zhang J, et al. Modulation of cardiac gap junction expression and arrhythmic susceptibility. Circ Res 2004;95:1035–41.
  18. Lombaert H, Peyrat JM, Croisille P, et al. Human atlas of the cardiac fiber architecture: study on a healthy population. IEEE Trans Med Imaging 2012;31:1436–47.
  19. Niederer SA, Plank G, Chinchapatnam P, et al. Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovasc Res 2011;89:336–43.
  20. Potse M, Krause D, Murzilli R, et al. Patient-specific modeling of cardiac electrophysiology in heart-failure patients. Europace 2014;16:iv56–61.
  21. Arts T, Reneman RS, Veenstra PC. A model of the mechanics of the left ventricle. Ann Biomed Eng 1979;7:299–318.
  22. Bovendeerd PHM. The mechanics of the normal and ischemic left ventricle during the cardiac cycle. A numerical and experimental analysis. Maastricht University: doctoral thesis, 1990.
  23. Bovendeerd PHM, Arts T, Delhaas T, et al. Regional wall mechanics in the ischemic left ventricle: numerical modeling and dog experiments. Am J Physiol 1996;270:H398–410.
  24. Arts T, Bovendeerd PHM, Prinzen FW, Reneman RS. Relation between left ventricular cavity pressure and volume and systolic fiber stress and strain in the wall. Biophys J 1991;59:93–102.
  25. Arts T, Delhaas T, Bovendeerd P, et al. Implementing adaptation rules results in self-shaping of heart and circulation, the CircAdapt model. Am J Physiol 2005;288:H1943–54.
  26. Lumens J, Delhaas T, Kirn B, Arts T. Three-wall segment (TriSeg) model describing mechanics and hemodynamics of ventricular interaction. Ann Biomed Eng 2009;37:2234–55.
  27. Lumens J, Arts T, Broers B, et al. Right ventricular free wall pacing improves cardiac pump function in severe pulmonary arterial hypertension: a computer simulation analysis. Am J Physiol Heart Circ Physiol 2009;297:H2196–205.
  28. Lumens J, Ploux S, Strik M, et al. Comparative electromechanical and hemodynamic effects of left ventricular and biventricular pacing in dyssynchronous heart failure: electrical resynchronization versus left–right ventricular interaction. J Am Coll Cardiol 2013;62:2395–403.
  29. Kerckhoffs RC, Faris OP, Bovendeerd PH, et al. Electromechanics of paced left ventricle simulated by straightforward mathematical model: comparison with experiments. Am J Physiol Heart Circ Physiol 2005;289:H1889–97.
  30. Niederer SA, Lamata P, Plank G, et al. Analyses of the redistribution of work following cardiac resynchronisation therapy in a patient specific model. PLoS One 2012;7:e43504.
  31. LeGrice IJ, Smaill BH, Chai LZ, et al. Laminar structure of the heart: ventricular myocyte arrangement and connective tissue architecture in the dog. Am J Physiol 1995;269:H571–82.
  32. Pluijmert M, Bovendeerd PH, Kroon W, et al. Effects of activation pattern and active stress development on myocardial shear in a model with adaptive myofiber reorientation. Am J Physiol Heart Circ Physiol 2014;306:H538–46.
  33. Prinzen FW, Augustijn CH, Arts T, et al. Redistribution of myocardial fiber strain and blood flow by asynchronous activation. Am J Physiol 1990;259:H300–8.
  34. Prinzen FW, Hunter WC, Wyman BT, McVeigh ER. Mapping of regional myocardial strain and work during ventricular pacing: experimental study using Magnetic Resonance Imaging tagging. J Am Coll Cardiol 1999;33:1735–42.
  35. Leenders GE, Lumens J, Cramer MJ, et al. Septal deformation patterns delineate mechanical dyssynchrony and regional differences in contractility: analysis of patient data using a computer model. Circ Heart Fail 2012;5:87–96.
  36. Lumens J, Leenders GE, Cramer MJ, et al. Mechanistic evaluation of echocardiographic dyssynchrony indices: patient data combined with multiscale computer simulations. Circ Cardiovasc Imaging 2012;5:491–9.
  37. Usyk TP, McCulloch AD. Electromechanical model of cardiac resynchronization in the dilated failing heart with left bundle branch block. J Electrocardiol 2003;36(Suppl):57–61.
  38. Kerckhoffs RC, Faris OP, Bovendeerd PH, et al. Timing of depolarization and contraction in the paced canine left ventricle: model and experiment, J Cardiovasc Electrophysiol 2003;14:S188–95.
  39. Kerckhoffs R, Omens JH, McCulloch AD, Mulligan LJ. Ventricular dilation and electrical dyssynchrony synergistically increase regional mechanical non-uniformity but not mechanical dyssynchrony: a computational model, Circ Heart Fail 2010;3:528–36.
  40. Bilchick KC, Dimaano V, Wu KC, et al. Cardiac magnetic resonance assessment of dyssynchrony and myocardial scar predicts function class improvement following cardiac resynchronization therapy. JACC Cardiovasc Imaging 2008;1:561–8.
  41. Kirn B, Jansen A, Bracke F, et al. Mechanical discoordination rather than dyssynchrony predicts reverse remodeling upon cardiac resynchronization. Am J Physiol 2008;295:H640–6.
  42. Kerckhoffs RC, Omens JH, McCulloch AD, Mulligan LJ. Ventricular dilation and electrical dyssynchrony synergistically increase regional mechanical nonuniformity but not mechanical dyssynchrony: a computational model. Circ Heart Fail 2010;3:528–36.
  43. Maréchaux S, Guiot A, Castel AL, et al. Relationship between two-dimensional speckle-tracking septal strain and response to cardiac resynchronization therapy in patients with left ventricular dysfunction and left bundle branch block: A prospective pilot study. J Am Soc Echocardiogr 2014;27:501–11.
  44. Trayanova NA, Constantino J, Gurev V. Electromechanical models of the ventricles. Am J Physiol Heart Circ Physiol 2011;301:H279–86.
  45. Rice JJ, Wang F, Bers DM, de Tombe PP. Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys J 2008;95:2368–90.
  46. Niederer SA, Hunter PJ, Smith NP. A quantitative analysis of cardiac myocyte relaxation: A simulation study. Biophys J 2006;90:1697–722.
  47. Kohl P, Sachs F. Mechanoelectric feedback in cardiac cells, Phil Trans R Soc Lond 2001;359:1173–85.
  48. Hermeling E, Delhaas T, Prinzen FW, Kuijpers NHL. Mechano electrical feedback explains T-wave morphology and optimizes cardiac pump function: insight from a multiscale model. Prog Biophys Mol Biol 2012;110:359–71.
  49. Kuijpers NH, Hermeling E, Lumens J. Mechano-electrical coupling as framework for understanding functional remodeling during LBBB and CRT. Am J Physiol Heart Circ Physiol 2014;306:H1644–59.
  50. Prinzen FW, Augustijn CH, Allessie MA, et al. The time sequence of electrical and mechanical activation during spontaneous beating and ectopic stimulation. Eur Heart J 1992;13:535–43.
  51. Ashikaga H, Coppola BA, Hopenfeld B, et al. Transmural dispersion of myofiber mechanics: implications for electrical heterogeneity in vivo. J Am Coll Cardiol 2007;27:909–16.
  52. Russell K, Smiseth OA, Gjesdal O, et al. Mechanism of prolonged electromechanical delay in late activated myocardium during left bundle branch block. Am J Physiol Heart Circ Physiol 2011;301:H2334–443.
  53. Russell K, Opdahl A, Remme EW, et al. Evaluation of left ventricular dyssynchrony by onset of active myocardial force generation: a novel method which differentiates between electrical and mechanical etiologies. Circ Cardiovasc Imaging 2010;3:405–14.
  54. Kerckhoffs RC, McCulloch AD, Omens JH, Mulligan LJ. Effects of biventricular pacing and scar size in a computational model of the failing heart with left bundle branch block. Med Image Anal 2009;13:362–9.
  55. Niederer SA, Shetty AK, Plank G, et al. Biophysical modeling to simulate the response to multisite left ventricular stimulation using a quadripolar pacing lead. Pacing Clin Electrophysiol 2012;35:204–14.
  56. Vernooy K, Verbeek XA, Peschar M, et al. Left bundle branch block induces ventricular remodelling and functional septal hypoperfusion. Eur Heart J 2005;26:91–8.
  57. Vernooy K, Cornelussen RN, Verbeek XA, et al. Cardiac resynchronization therapy cures dyssynchronopathy in canine left bundle-branch block hearts. Eur Heart J 2007;28:2148–55.
Previous Volume Article